Тест по алгебре
Поделиться:
1. При каком, выраженном через а и b, значении m выражение будет полным квадратом?
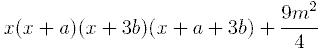
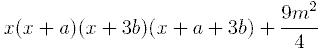
- 1. 4/9a2b2
- 2. ±3/2ab
- 3. 9/4a2b2
- 4. Правильный ответ не приведен
2. Решите неравенство:
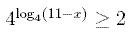
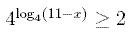
- 1. х = 9
- 2. 9 ≤ х < 11
- 3. х ≤ 8
- 4. х ≤ 9
3. Составьте квадратное уравнение, корни которого обратны корням уравнения х2 - 20х + 96 = 0.
- 1. 96х2 + 20х + 1 = 0
- 2. 96х2 - 20х + 1 = 0
- 3. 96х2 - 20х - 1 = 0
- 4. 96х2 + 20х - 1 = 0
4. При каких значениях х верно равенство |x2 - 49| = 49 - х2?
- 1. -7 ≤ х ≤ 7
- 2. х ≥ 7
- 3. х ≤ -7
- 4. х ≤ 7
5. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 4+√5 и 4-√5.
- 1. 20
- 2. -18
- 3. 4
- 4. -2
6. Один из корней квадратного уравнения х2 + 11х + q = 0 равен 8. Найдите второй корень.
- 1. -152
- 2. 19
- 3. -3
- 4. -19
7. Найдите значение x1x22 + x21x2, если x1 и х2 - корни квадратного уравнения х2 - 8х + 11 = 0.
- 1. -168
- 2. 88
- 3. -78
- 4. -88
8. Найдите значение x2 + x2x1 + x1, если x1 и х2 - корни квадратного уравнения 2х2 + 5х - 11 = 0.
- 1. -8
- 2. -7
- 3. -3
- 4. -6
9. Найдите значение x2 + x2x1 + x1, если x1 и х2 - корни квадратного уравнения 2х2 + 3х - 7 = 0.
- 1. -2
- 2. -4
- 3. -5
- 4. -7
10. Найдите значение x2 + x2x1 + x1, если x1 и х2 - корни квадратного уравнения 2х2 + 7х - 3 = 0.
- 1. -2
- 2. -4
- 3. -3
- 4. -5
11. Найдите значение x2 + x2x1 + x1, если x1 и х2 - корни квадратного уравнения 2х2 - 5х + 3 = 0.
- 1. 0
- 2. -4
- 3. -1
- 4. 4
12. Один из корней квадратного уравнения х2 - 11х + q = 0 равен 8. Найдите второй корень.
- 1. -24
- 2. 19
- 3. -3
- 4. 3
13. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 5+√3 и 5-√3.
- 1. 13
- 2. 23
- 3. -21
- 4. -1
14. Один из корней квадратного уравнения х2 + 13х + q = 0 равен 7. Найдите второй корень.
- 1. 20
- 2. 6
- 3. -140
- 4. -20
15. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 6+√2 и 6-√2.
- 1. 23
- 2. -35
- 3. 47
- 4. -21
16. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 3+√5 и 3-√5.
- 1. -9
- 2. -1
- 3. 11
- 4. 3
17. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 4+√3 и 4-√3.
- 1. -20
- 2. 6
- 3. 22
- 4. -4
18. Составьте квадратное уравнение, корни которого равны 6+√3 и 6-√3.
- 1. х2 + 12х - 33 = 0
- 2. х2 - 12х - 33 = 0
- 3. х2 + 12х + 33 = 0
- 4. х2 - 12х + 33 = 0
19. Составьте квадратное уравнение, корни которого равны 4+√5 и 4-√5.
- 1. х2 - 8х - 11 = 0
- 2. х2 + 8х - 11 = 0
- 3. х2 - 8х + 11 = 0
- 4. х2 + 8х + 11 = 0
20. Составьте квадратное уравнение, корни которого равны 3+√2 и 3-√2.
- 1. х2 - 6х - 7 = 0
- 2. х2 + 6х + 7 = 0
- 3. х2 - 6х + 7 = 0
- 4. х2 + 6х - 7 = 0
21. Составьте квадратное уравнение, корни которого равны 2+√5 и 2-√5.
- 1. х2 + 4х - 1 = 0
- 2. х2 - 4х - 1 = 0
- 3. х2 + 4х + 1 = 0
- 4. х2 - 4х + 1 = 0
22. Найдите значение x2 + x2x1 + x1, если x1 и х2 - корни квадратного уравнения 2х2 + 5х - 3 = 0.
- 1. 2
- 2. 4
- 3. 1
- 4. -4
23. Найдите значение x1x22 + x21x2, если x1 и х2 - корни квадратного уравнения х2 - 10х + 22 = 0.
- 1. -120
- 2. 220
- 3. 280
- 4. -220
24. Один из корней квадратного уравнения х2 - 13х + q = 0 равен 7. Найдите второй корень.
- 1. 20
- 2. -42
- 3. -6
- 4. 6
25. Один из корней квадратного уравнения х2 - 7х + q = 0 равен 11. Найдите второй корень.
- 1. 18
- 2. -4
- 3. 44
- 4. 4
26. Найдите значение x1x22 + x21x2, если x1 и х2 - корни квадратного уравнения х2 - 8х + 13 = 0.
- 1. 104
- 2. 94
- 3. -152
- 4. -104
27. Найдите значение x1x22 + x21x2, если x1 и х2 - корни квадратного уравнения х2 - 6х + 7 = 0.
- 1. 42
- 2. 77
- 3. -32
- 4. -42
28. Найдите значение x1x22 + x21x2, если x1 и х2 - корни квадратного уравнения х2 - 8х + 14 = 0.
- 1. -112
- 2. 112
- 3. -144
- 4. -92
29. Составьте квадратное уравнение, корни которого равны 2+√3 и 2-√3.
- 1. х2 + 4х + 1 = 0
- 2. х2 + 4х - 1 = 0
- 3. х2 - 4х - 1 = 0
- 4. х2 - 4х + 1 = 0
30. Найдите наименьшее целое значение k, при котором уравнение х2 - 2(k + 2)х + 11 + k2 = 0 имеет два различных действительных корня.
- 1. 1
- 2. -2
- 3. -1
- 4. 2
31. Найдите сумму корней уравнения:
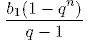
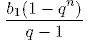
- 1. 3
- 2. -4
- 3. -3
- 4. 4
32. При каких значениях t уравнение х2 + (t - 2)х + 4 = 0 имеет два различных отрицательных корня?
- 1. t ≤ 1
- 2. t > 6
- 3. t < 1
- 4. t < 2
33. Корни уравнения х2 + рх + q = 0 вдвое больше корней уравнения х2 - 3х + 2 = 0. Чему равно р + q?
- 1. 2
- 2. -2
- 3. 14
- 4. -14
34. Найдите сумму корней уравнения:
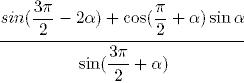
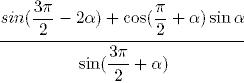
- 1. 3
- 2. -5
- 3. 6
- 4. -3
35. Найдите разность наибольшего и наименьшего корней уравнения х4 - 10х2 + 9 = 0.
- 1. 2
- 2. 8
- 3. 1
- 4. 6
36. Зная, что x1 и х2 - корни уравнения х2 + х - 1 = 0, найдите х31+х32.
- 1. 2
- 2. -1
- 3. 3
- 4. -4
37. Найдите наибольшее целое значение k, при котором уравнение kz2 + 2(k - 12)z + 6/5 = 0 не имеет действительных корней.
- 1. 20
- 2. 18
- 3. 16
- 4. 17
38. Сколько целых решений имеет уравнение |x2 - 3х| = 3х - х2?
- 1. 1
- 2. 2
- 3. 3
- 4. 4
39. Зная, что x1 и х2 - корни уравнения х2 - х + q = 0. Найдите q, если x31 + х32 = 19.
- 1. -12
- 2. -2
- 3. -5
- 4. -6
40. Найдите сумму корней уравнения |х| = х2 - х - 4.
- 1. 1 — 2√5
- 2. 2 - √5
- 3. —1 + √5
- 4. 1 + √5
41. x1 и х2 - корни уравнения x2 + mx + n = 0. Если каждый корень этого уравнения увеличить на 4 и из полученных чисел составить новое уравнение, то свободный член нового уравнения будет равен n - 32 (n - свободный член исходного уравнения). Чему будет равно m?
- 1. 9
- 2. 11
- 3. 10
- 4. 12
42. Найдите наибольшее значение выражения 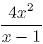 , если
, если 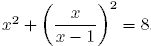 .
.
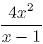 , если
, если 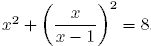 .
.- 1. 8
- 2. 4
- 3. 2
- 4. 16
43. Вычислите x1/х2 + x2/х1, если x1 и х2 - корни уравнения 3х2 - 8х - 15 = 0.
- 1. -3 19/45
- 2. -3 1/45
- 3. 5
- 4. -8/3
44. При каких значениях а уравнение ах2 - (а + 1)х + 2а + 2 = 0 имеет один корень?
- 1. 0; -1
- 2. -1; 0; 1/7
- 3. 1; -1/7
- 4. -1; 1/7
45. Чему равна сумма всех натуральных чисел, являющихся корнями уравнения |х2 - 8х + 7| = -7 + 8х - х2?
- 1. 40
- 2. 8
- 3. 25
- 4. 28
46. При каких значениях k уравнение х2 – 2k(х + 1) – k2 + 6k = 0 имеет отличное от нуля два совпадающих корня?
- 1. 1
- 2. -2
- 3. 2
- 4. -1
47. z1 и z2 - корни уравнения z2 + pz + q = 0. Если каждый корень этого уравнения увеличить на 4 и из полученных чисел составить новое уравнение, то свободный его член будет равен q + 68. Найдите р.
- 1. -10
- 2. -14
- 3. -13
- 4. -11
48. Найдите k в уравнении х2 + 3х + k + 8 = 0, если его корни x1 и х2 удовлетворяют условию x1/х2 = -1/4.
- 1. -10
- 2. -12
- 3. -7
- 4. -8
49. Найдите произведение корней уравнения .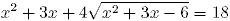
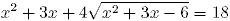
- 1. -10
- 2. 0
- 3. 390
- 4. 3
50. Найдите произведение корней уравнения 4|х - 2| = 3 + (х - 2)2.
- 1. -3
- 2. 3
- 3. 15
- 4. -15