Сколько корней имеет уравнение 4cos(x/2) + cosх + 1 = 0 на [0; 9,5π]?
5
3
1
2
Также изучают: Элементарная математика, Алгебра, Итоговый тест (11 класс), географическое положение России (8 класс), знание политической карты мира
Сколько корней имеет уравнение 4cos(x/2) + cosх + 1 = 0 на [0; 9,5π]?
5
3
1
2
Решите неравенство: tg(x – π/4) ≤ -1.
[-π/2 + πk; π/4 + πk), k Є Z
(-π/4 + πk; πk], k Є Z
[π/4 + 2πk; π/2 + 2πk], k Є Z
[πk; 3π/4 + πk), k Є Z
Решите уравнение: tgx·tg3x = -1.
πk/2, k Є Z
π/4 + πk, k Є Z
π/4 + πk/2, k Є Z
πk, k Є Z
Укажите количество корней уравнения на промежутке [0; 4π]: sin2x + sinx = 0 cosx
7
5
2
4
При каких значениях х верно неравенство cos2х – 5/2 cosх + 1 ≤ 0 х Є [0; 2π] ?
[5π/3; 2π]
[0; π/3]
[0; π/3] U [5π/3; 2π]
[π/3; π/2] U [3π/2; 5π/3]
Решите уравнение: tgx – tg(π/3) - tgx·tg(π/3) = 1.
7π/12 + 2πk, k Є Z
5π/6 + 2πk, k Є Z
7π/6 + πk, k Є Z
7π/12 + πk, k Є Z
Сколько корней уравнения (3sinπх - π) · (2cosπx - 1) = 0 принадлежат промежутку [0; 3]?
3
1
2
4
Решите уравнение: √cosx · sinx = 0.
2πk; π/2 + πk, k Є Z
π/2 + πk, k Є Z
πk, k Є Z
π/2 + 2πk, k Є Z
При каких значениях х верно неравенство sin2х – 5/2 sinx + 1 < 0, если х Є [0; 2π]?
(π/6; 5π/6)
[0; π/6) U (5π/6; 2π]
(0; π/3) U (2π/3; 2π]
[0; π/3] U [2π/3; 2π]
Решите неравенство: 4cos2х - 3 ≥ 0.
[-π/6 + πk; π/6 + πk], k Є Z
[-π/3 + πk; π/3 + πk], k Є Z
[-π/3 + 2πk; π/3 + 2πk], k Є Z
[-π/6 + 2πk; π/6 + 2πk], k Є Z
Сколько корней имеет уравнение на промежутке [—2π; 2π]?
cos2x – cosx = 0 sinx
4
3
2
6
Решите уравнение: √sinx · cosx = 0.
π/2 + 2πk, k Є Z
π/2 + πk, k Є Z
πk, k Є Z
π/2 + 2πk; πk, k Є Z
Сколько корней имеет уравнение на промежутке [0; 5π] ?
ctgx = 0 1 + sinx
5
2
4
3
Найдите корень уравнения ctg(х + 1) · tg(2х - 3) = 1 принадлежащий промежутку (π; 2π).
5
2
3
4
Найдите наименьший положительный корень уравнения:
(3cosπx - π) · (2sinπx - √3) = 0.
π/6
1/4
1/3
1/2
Решите уравнение: sin2х + tgх = 2.
π/4 + πk, k Є Z
-π/4 + πk, k Є Z
-π/6 + πk/2, k Є Z
π/6 + πk/2, k Є Z
Решите неравенство: |sinх| ≤ √3 2
[-π/6 + 2πk; π/6 + 2πk], k Є Z
[-π/3 + πk; π/3 + πk], k Є Z
[-π/6 + πk; π/6 + πk], k Є Z
[-π/3 + 2πk; π/3 + 2πk], k Є Z
Решите систему: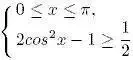
[0; π/6] U [5π/6; π]
[0; 2π/3]
[0; π/3]
[2π/3; π]
Также изучают: Элементарная математика, Алгебра, Итоговый тест (11 класс), географическое положение России (8 класс), знание политической карты мира
*и немного немецкого автопрома
Скажу сразу, что в этой статье нет ни грамотного определения предела функции, ни достаточного количества разнообразных примеров, ни правил и основных приёмов определения предела. Всё это можно и нужно читать в учебниках и задачниках. Цель этой статьи – помочь понять смысл, суть, скрывающуюся за цифрами, правилами и терминами.

Предел функции f(x) в какой-либо точке х0 – это значение, к которому она стремится при стремлении x к значению х0
В это грубое, неверное с точки зрения математики, определение криво,но вписывается сама суть предела функции. Если разобраться с ним, то потом можно и разбираться во всех тонкостях, которые вполне подробно описаны в учебниках.
Важно разобраться буквально с каждым словом в определении, в этом есть ключ к осознанию определения. Стремление – вот один из основных терминов в определении. Стремление – это максимально возможное приближение. То есть стремление х к какому-либо конкретному значению (обозначаемому как х0, если кто не понял) – это максимальное приближение х к данному значению. В простом случае, если функция имеет значение в точке х0 , то максимально возможное приближение, и есть х0 .
А если при х0 функция не существует? Придётся говорить несколько иначе. А иначе говоря, стремление – это минимальное отличие. Что такое минимальное отличие? Минимальное отличие, это отличие на минимальную величину, на минимальное число. Какое число будет являться минимальным? 0 сразу отбросим, так как отличия на 0 не бывает, если два числа отличаются на 0, то они совпадают, этот случай мы уже описали. Тогда какое это число? 0.1, 0.0001, 0.000000000000000000000000000000001? Но мы всегда можем добавить пару-тройку нолей после запятой и тем самым уменьшить число на несколько порядков, и уменьшать мы можем бесконечно, ну или пока не умрём. Вот тут мы подошли к важному моменту. Товарищи математики в этом случае придумали такую штуку как «Бесконечно Малая Величина» (далее БМВ (= ). БМВ – это величина, которая по модулю меньше любого наперёд заданного числа. Это значит, что для числа 10000 мы можем считать бесконечно малой 0.1, но как только мы озвучили «0.1» БМВ стала 0.0000001 и снова мы озвучили значение БМВ и она стала ещё меньше, например 0.000000000000001, и мы снова это сделали, мы озвучили её значение и она стала… не буду повторять, вы поняли. Она всегда меньше любого озвученного числа, в этом и есть вся магия. Возвращаясь к нашей функции и х0 , в котором она не имеет значения, отметим, что при всех других, хоть сколько-нибудь отличающихся от х0 значениях, она существует, даже если это отличие на БМВ. То есть, если функция при х0 не существует, то стремление х к х0 есть отличие значения х от х0 на БМВ. Подводя черту скажем, что стремление х к х0 – это либо само х0 (если f(x) существует в х0), либо значение, отличающееся от х0 на БМВ (х0±БМВ) (если f(x) не существует в х0 ).
Допустим, есть у нас функция f(x)=3x-1, данная функция определена на всём промежутке по оси х (выражение 3х-1 можно вычислить для любого значения х), следовательно, никаких проблемных мест нет и мы всегда можем вычислить предел данной функции, просто подставив вместо х интересующее нас значение. Если нас интересует предел функции при стремлении х к конечному значению, то всё просто (см. выше):
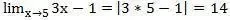
Если нас интересует стремление х в бесконечность, то нам всегда поможет простое рассуждение:
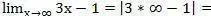
Логично, что если умножить любое конечное число на бесконечно большую величину, оно станет бесконечно большим; а если отнять от бесконечно большого числа конечное число, то оно останется бесконечно большим:
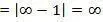
Допустим, функция f(x) выглядит, как представленно ниже:
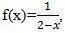
Данная функция определена не на всём промежутке по оси х (при х=2 знаменатель дроби обращается в 0, а деление на ноль обращает всё сущее в прах и никто на ноль поэтому не делит), поэтому наиболее интересен предел функции при стремлении х к 2.
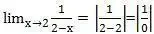
Отметим, что 0 здесь это не «ноль» а БМВ, так как на самом деле мы вместо х подставляем не «два», а число, отличающееся от двух на БМВ; кроме того, логично, что если поделить конечное число на бесконечно малое, то оно возрастёт в бесконечное число раз и станет бесконечно большим (попробуйте поделить 2 на 0,0000000000000001)
Если быть более строгим (что правильно), то стремление х к конкретному значению может быть как с большей, так и с меньшей стороны, в описанном выше примере это приводит к двум случаям (обозначим «2+БМВ» как «2+» (стремление с большей стороны), а «2-БМВ» как «2-»(стремление с меньшей стороны)): 2-2+=-0; 2-2-= 0 – (снова, 0 здесь, это БМВ), следовательно и конечный результат для каждого случая будет иметь значения + бесконечность и - бесконечность. Этот случай иллюстрирует пример предела справа и предела слева, используемые для таких ситуёвин:
Кроме того, отличаются пределы и при стремлении х к любой из бесконечностей. Всё это легко проследить на графике:
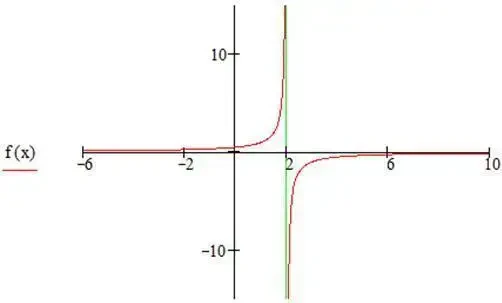
На этом статья себя уже исчерпала, всё остальное (включая правильное определение предела функции) ищите в учебниках по высшей математике.